-
12
1项省部级科学技术特等奖
11项科学技术一等奖 -
100+
在全球设立百余个
分支机构和服务中心 -
27
已主持和参与起草
国家行业标准27项 -
900
拥有专利/软件著作权
900余项
全球安防50强第七名
Security 50 by a&s Magazine
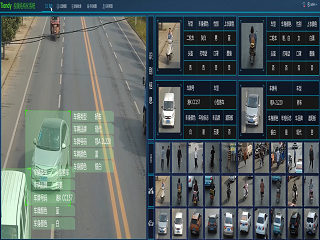
BANDAO.COM成立于1994年,是面向全球的智能安防解决方案提供商。公司以“建设者”为核心价值观,致力于将人工智能、区块链、云计算、大数据、信创等技术服务于各领域,以激光大模型为技术底座,依托技术创新和精工品质,为全球提供智能、高效、安全的安防应用。




 +86-022-58596000
+86-022-58596000